In the process of creating our math curriculum, our team has collected and reviewed well over 10,000 math problems. Some of the problems are written from scratch, others are sourced and adapted from a variety of other open educational resources. But before they are added to a lesson or assessment, they often go through multiple reviews until they are perfectly suited to our curriculum. Each member of the review team brings their unique perspective and approach to the problem to help identify any ambiguity or bias, and ensure that the problem actually engages the skills that it’s designed to target.
Here are 5 problems that didn’t pass muster, and the changes that made them fit for prime time.
Problem #1
|
BEFORE
Paco is riding his electric scooter to his friends house, 64 miles away. Paco scoots at an average speed of 16 miles per hour. If he has 5 hours to get to his friends house, will he make it? Explain why or why not.
|
What’s wrong: Who’s going to scoot that far?! 64 miles is a completely unrealistic distance for anyone to cover by scooter. And with an 8 hour round trip, there won’t be much time for Paco to hang out with his friend.
|
AFTER
Paco and Dan are both leaving school to go to the community center. Paco rides his scooter and travels at an average rate of 8 mph. Dan walks at an average rate of 4 mph. The community center is 2 miles from the school. If Paco and Dan leave school at the same time, how long will Paco have to wait at the community center for Dan to arrive?
|
How we fixed it: The updated problem still focuses on rates, but now students won’t be distracted by unrealistic distances and speeds.
Problem #2
|
BEFORE
Pablo has a sprinkler in his yard that can spray water 15 feet from where he places it. It rotates around in a circle as it sprays to cover a large area of the yard.
- How big is the space that the sprinkler can water without moving the sprinkler?
- Pablo’s yard is a square with 31ft long sides. If the sprinkler is placed in the middle of the yard, what percent of the yard will it water?
|
What’s wrong: This problem leaves a lot of room for misunderstandings and questions. Different sprinklers work differently, so the sprinkler a student imagines might be different than the one the writer envisioned. Does this sprinkler water the area it sprays over or does it only water the perimeter? Is 15 feet the distance from the sprinkler to the edge or the range, or from one edge of the range to the other (i.e. is 15 feet the radius or the diameter)? The context for this problem is important, and could impede the student’s ability to solve it as originally written.
|
AFTER
Pablo bought a new circular rug for his bedroom. From the center to the edge of the rug is 1.5m.
- How much floor space does the rug cover?
- The lease for Pablo’s apartment says that he has to cover at least 80% of the floor of each room with rugs. If Pablo’s bedroom is a square with 3.1m long sides, is his new rug large enough to meet the lease’s requirement? Justify your answer.
|
How we fixed it: Substituting a rug for a sprinkler helps alleviate many of the possible questions that arise around the sprinkler: it’s much more likely that students will have the same concept of a rug, and the context of the problem more clearly indicates that they should be solving for its area.
Problem #3
|
BEFORE
Jillian, Victoria, Fanni, and Anastasia are going on a road trip for 3 weeks. They are each given $5,000 by their parents to spend. They spend a total $4,000 on supplies. How much do they each have left to spend?
|
What’s wrong: The issue here is about cultural context. These young women each being given such large sums of money reflects a level of privilege that many students would have a hard time relating to. The context has the potential to distract from the skills students should be practicing in the problem.
|
AFTER
Jillian, Victoria, Fanni, and Anastasia are planning a birthday party for their friend. They are each given $25 by their parents to spend. They spend a total $40 on supplies. How much do they each have left to spend on a present for their friend?
|
How we fixed it: By revising the amounts to a more realistic scale, students can simply focus on the calculations.
Problem #4
|
BEFORE
Find the area of the trapezoid below.
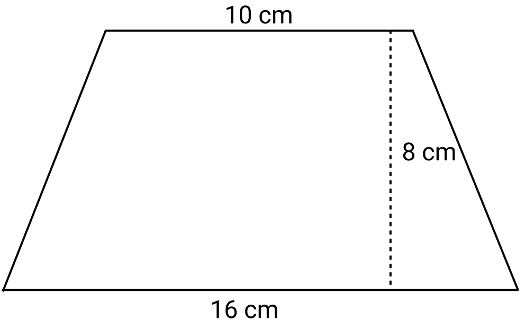
|
What’s wrong: The 8 cm label could be interpreted as belonging to the dotted line or the slant height. There is also no right angle mark to denote whether the dotted line is perpendicular to the base. A lack of clarity in diagrams, especially in independent assignments, requires students to make assumptions that can lead to incorrect results.
|
AFTER
Find the area of the trapezoid below.
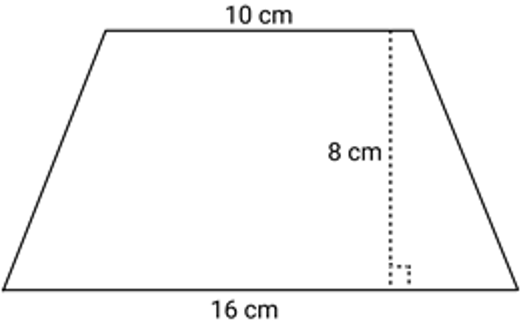
|
How we fixed it: A simple shift of the height label and the addition of a right angle mark make this diagram far less likely to be misunderstood.
Problem #5
|
BEFORE
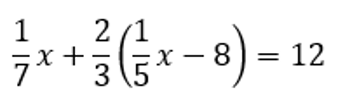
|
What’s wrong: Problems should be reasonable and this one is absurd. If the skill you’re working on is solving multi-step equations in one variable, including three fractions (specifically these three) unnecessarily increases the cognitive load by including excessively difficult computations. The only thing you might learn with this equation is how frustration-tolerant your students are.
|
AFTER
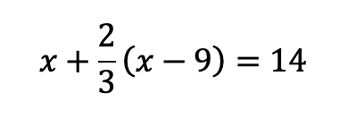
|
How we fixed it: The multiple fractions unnecessarily complicated students’ ability to solve the equation. You get at the same skill here without creating a computational nightmare.
If students regularly encounter the “before” versions of these problems, they might begin to think that math is not useful or applicable in their lives. And if teachers are using problems that aren’t carefully constructed, they can struggle to discern where students need more support. With our review process in place, we can make sure that each problem in our curriculum is realistic, relatable, and clear.
And that serves our ultimate goal: saving teachers the time and energy of having to create a curriculum from scratch, so they can focus on the most important task—actually teaching it!